4주차는 뉴럴 네트워크에 관한 내용입니다. 이번 단원에서는 직관적으로 뉴럴 네트워크의 이론을 이해하는 단원입니다. 저는 neural network 가 효율적으로 표현할 수 있는 non-linear 가설의 예시가 좋았습니다.
Neural network 를 벡터로 표현하기
$$a_1^{(2)} = g(\Theta_{10}^{(1)} x_0 + \Theta_{11}^{(1)} x_1 + \Theta_{12}^{(1)} x_2 + \Theta_{13}^{(1)} x_3) $$
$$a_2^{(2)} = g(\Theta_{20}^{(1)} x_0 + \Theta_{21}^{(1)} x_1 + \Theta_{22}^{(1)} x_2 + \Theta_{23}^{(1)} x_3) $$
$$a_3^{(2)} = g(\Theta_{30}^{(1)} x_0 + \Theta_{31}^{(1)} x_1 + \Theta_{32}^{(1)} x_2 + \Theta_{33}^{(1)} x_3) $$
$$h_{\Theta} (x) = g(\Theta_{10}^{(2)} a_0^{(2)} + \Theta_{11}^{(2)} a_1^{(2)} + \Theta_{12}^{(2)} a_2^{(2)} + \Theta_{13}^{(2)} a_3^{(2)}) $$
where $a^{(1)} = x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix}$
and let
$z_1^{(2)} = \Theta_{10}^{(1)} x_0 + \Theta_{11}^{(1)} x_1 + \Theta_{12}^{(1)} x_2 + \Theta_{13}^{(1)} x_3$,
$z_2^{(2)} = \Theta_{20}^{(1)} x_0 + \Theta_{21}^{(1)} x_1 + \Theta_{22}^{(1)} x_2 + \Theta_{23}^{(1)} x_3$,
$z_3^{(2)} = \Theta_{30}^{(1)} x_0 + \Theta_{31}^{(1)} x_1 + \Theta_{32}^{(1)} x_2 + \Theta_{33}^{(1)} x_3$,
$z^{(3)} = \Theta_{10}^{(2)} a_0^{(2)} + \Theta_{11}^{(2)} a_1^{(2)} + \Theta_{12}^{(2)} a_2^{(2)} + \Theta_{13}^{(2)} a_3^{(2)}$
$h_{\Theta} (x) = a^{(3)} = g ( z^{(3)} )$ 에서,
$z^{(3)} = \begin{bmatrix} \Theta_{10}^{(2)} & \Theta_{11}^{(2)} & \Theta_{12}^{(2)} & \Theta_{13}^{(2)} \end{bmatrix} \begin{bmatrix} a_0^{(2)} \\ a_1^{(2)} \\ a_2^{(2)} \\ a_3^{(2)} \end{bmatrix} = \Theta^{(2)} a^{(2)}$
그리고, $a_1^{(2)} = g ( \Theta^{(1)} x )$
where $ \Theta^{(1)} x = \begin{bmatrix} \Theta_{10}^{(1)} & \Theta_{11}^{(1)} & \Theta_{12}^{(1)} & \Theta_{13}^{(1)} \\ \Theta_{20}^{(1)} & \Theta_{21}^{(1)} & \Theta_{22}^{(1)} & \Theta_{23}^{(1)} \\ \Theta_{20}^{(1)} & \Theta_{21}^{(1)} & \Theta_{22}^{(1)} & \Theta_{23}^{(1)} \end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} $
예시
$y = x_1 \text{ XOR } x_2$ 를 구한다고 해봅시다.
| Input | Output | ||
| $x_1$ | $x_2$ | $x_1 \text{ XOR }x_2$ | |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| $x_1$ | $x_2$ | $a_1^{(2)}$ | $a_2^{(2)}$ | $h_\Theta (x)$ |
| 0 | 0 | 0 | ||
| 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 0 |
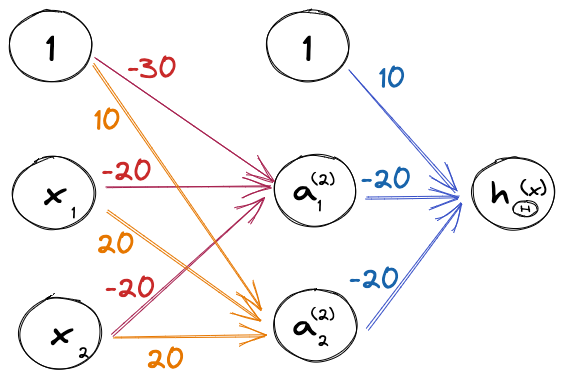
위 표의 빈칸에 맞는 값들을 찾아야 합니다. $h_{\Theta} (x)$ 값이 둘 다 $0$이 될 때와 $1$ 이 될 때 각각 $a_1^{(2)}$ 와 $a_2^{(2)}$ 의 규칙이 비슷해야 합니다. 그래서 저는 다음과 같은 방법을 생각해 보았습다. $a_1^{(2)}$ 와 $a_2^{(2)}$ 이 $0$ 또는 $1$ 일 때 $h_\Theta (x)$ 값이 $0$ 이 되고, 둘 다 $0$ 일 때 $h_\Theta (x)$ 값이 $0$ 이 됩니다. 이렇게 했을 때, $a_1^{(2)}$ 이 [0,0,0,1] 형태가 나오고, $a_2^{(2)}$ 이 [1,0,0,0] 형태가 나옵니다. $a_1^{(2)}$ 또는 $a_2^{(2)}$ 가 output 으로 $1$ 값을 가지는 상황이, input 인 $x_1$ 과 $x_2$ 가 둘 다 $0$ 일때나 둘 다 $1$ 일때와 관련이 있어서 $x_1 \text{ AND } x_2$ 또는 $(\text{ NOT } x_1) \text{ AND } (\text{ NOT } x_2)$ 로 표현이 가능해보입니다.
| $x_1$ | $x_2$ | $a_1^{(2)}$ | $a_2^{(2)}$ | $h_\Theta (x)$ |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
$h_\Theta (x)$ 가 output 인 상황:
$a_1^{(2)}$가 output 인 상황:
$a_2^{(2)}$가 output 인 상황:
종합하면, 아래 그림과 같다.
$y = 1$ 과 $y=0$ 을 반대로 했을 때 뉴럴 네트워크를 어떻게 구성해야 하는지 직접 풀어보면 좋은 연습이 될 것 같습니다. 정답은 Coursera 코스의 강좌 예제와 동일합니다 (이번 포스팅에 작성된 예제는 Coursera 코스 강좌에서 $y=1$ 과 $y=0$을 반대로 했을 때를 직접 풀어본 경우입니다).
Multiclass Classification
개, 고양이, 사람, 자동차 등의 여러 가지 사물로 분류할 때는, output 을 개 = [1,0,0,0], 고양이 = [0,1,0,0], 사람 = [0,0,1,1], 자동차 = [0,0,0,1] 이런 식으로 정의하고 한 번에 하나씩 위의 방식으로 파라미터를 구합니다.
어플리케이션
손글씨에서 숫자 (0~9) 구하기와 같은 것들이 대표적입니다. 손글씨에서 숫자 구하기의 경우에는 10개의 y 를 [1,...,0] 이런 식으로 정의하고 구합니다. 파이썬 말고 C++ 에서도 동작하는 그러한 코드를 작성해보고 싶다 (파이썬 라이브러리보다 속도가 더 빠르지 않을까 싶네요).